经过国际学者和工程界多年的发展，支付网络的几个子研究方向已经出现了大量的研究论文和工程实践，难以详细阅读和理解。区块链经常因为第1层的事务吞吐量上限而受到批评。离线支付渠道网络(PCN)提供了“离线支付在线结算”的解决方案，为区块链世界的支付(及其广义交互)提供了几乎无限的交易吞吐量。因此，支付网络成为区块链研究和工程实践中最热门的方向之一。

经过国际学者和工程界多年的发展，支付网络的几个子研究方向已经出现了大量的研究论文和工程实践，难以详细阅读和理解。然而，对于现阶段这一重要的研究方向，虽然区块链领域的大多数人对其基本思路有所了解，但国内全面跟踪其最新进展的极客和学者并不多。

本评论系列面向对该领域感兴趣的极客和学者。分析了几个分方向，总结了最新的研究进展，提出了作者的思考。作者是Shor，Nervos热爱研究的合作伙伴，现为上海交通大学博士。

在这篇文章中，我们的读者对离线支付网络默认有一个基本的了解。在一些描述中，我们将支付网络看作一个图，每个参与者看作一个顶点，每个支付渠道看作图上的一条边。所以作者会不自觉地指一个有“图”的支付网络，一个有“节点”的参与者，一个有“边”字的支付渠道。路由，即需要在支付网络上发送交易的人和交易的接收者与图上的其他节点交互来决定支付路径的过程。当然，严格来说，这不一定是一条路径，而是由一系列路径组成的有向无环图(DAG)。由于其他学者似乎没有对这一类别采用新的术语，作者将这一系列路径的总和命名为交易模式。

1基于网络流的路由协议用网络流模型描述支付网络的整体状态，具有以下优点：首先，网络流准确描述了每个支付通道的总量和余量，现有的最大流算法可以找到两点之间可以达到的最大支付量，高效地找到一组可行路径。接下来，作者简单介绍了网络流量问题。提示：“基于网络流的路由协议”是作者提出的名称，其在大多数文献中对应的短语是源路由。原因是这种路由过程必须由源节点在本地完成。在这个过程中，默认的源节点已经掌握了整个支付网络的拓扑结构，可以动态地探查任何支付渠道中的保证金。但是现有的source routing方案都是基于最大流算法的，所以作者大胆的把题目改了一下让读者理解(另一个主要原因是作者会提出一个基于网络流的路由协议，在研究前景中不属于Source Routing的范畴)。

网络流问题简介

，我们用网络流模型中的一个剩余网络来表示支付网络的整体配置，本质上是一个四元祖先，其中设置了节点，每个节点代表支付网络中的一个参与节点，这是一个边集，每个边代表一个支付通道，代表每个边的剩余流量。结合支付网络的应用需求，我们传统上增加了最大吞吐量(，)，这是在每个通道建立时建立的，不同于网络流量。最大流是网络流模型上的一族线性规划问题。从到()的单源单汇最大流量问题是：

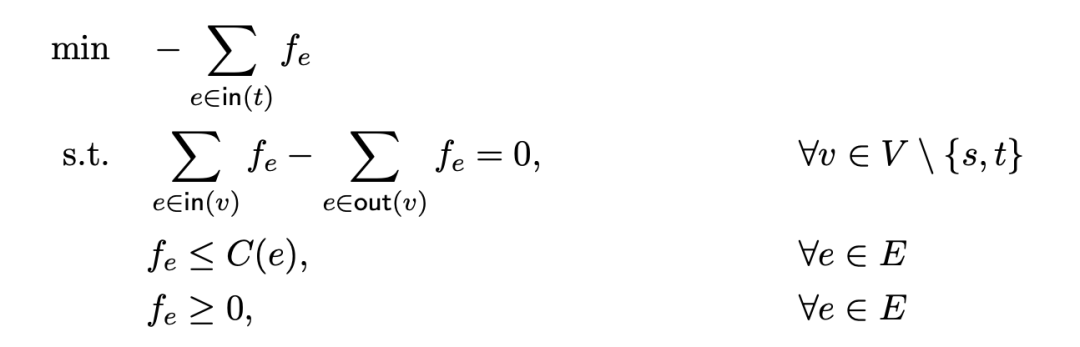
这种基于线性规划的严谨定义，不方便观众理解。作者画了以下图片，帮助读者理解最大流问题的定义。在下图中，最大流量以单位为单位。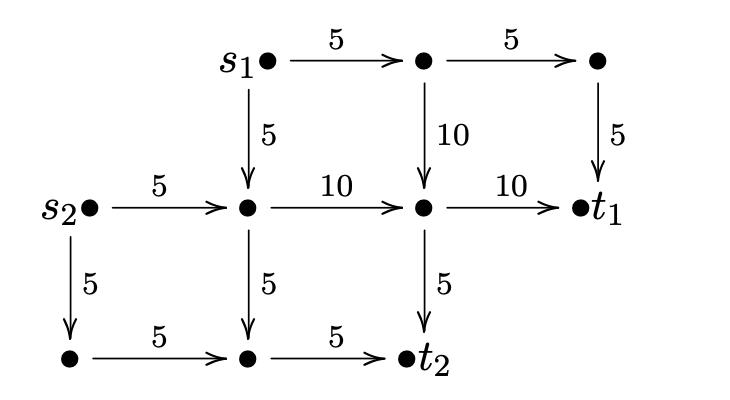

如果获得的单位的配额全部用完，则不仅有一个方案，而且其中一个“扩充”方案如下所示。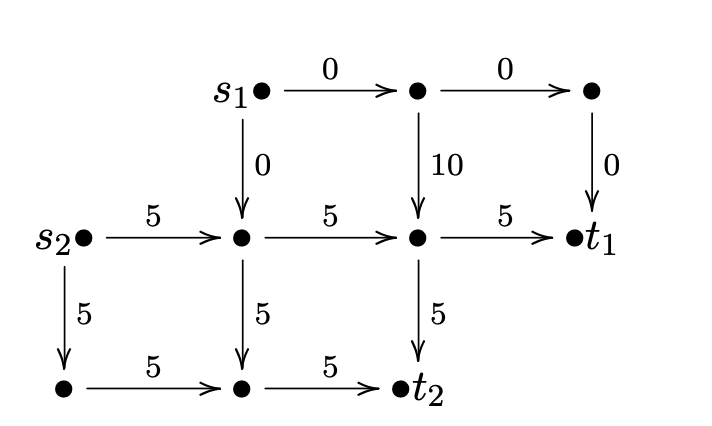

此时，最大流量仍为单位，但方案是独特的。如果单位流量刚好用完，整个图的剩余网络如下。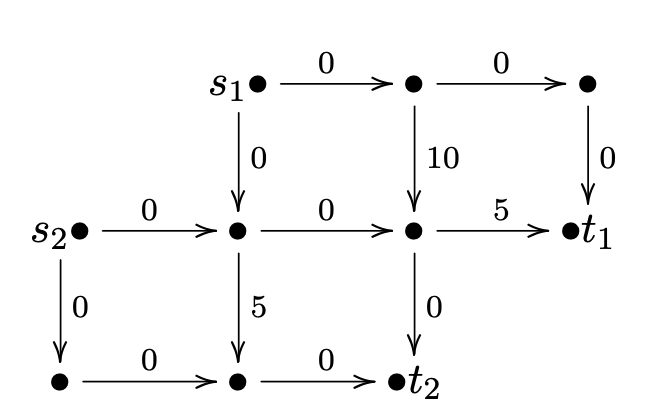

常用的最大流算法有预约推送算法(HLPP)和一类基于增广路径定理的最大流算法，包括埃德蒙兹-卡普算法及其衍生算法如ISAP算法和迪尼奇算法。这些算法在最坏的情况下具有极高的理论复杂度，以及相当大的运算效率，而运算效率往往远低于理论复杂度。比如考虑一个有节点边的交通图，Edmonds-Karp算法的理论计算复杂度和Dinic算法一样高，它们在正态稀疏随机图上的执行效率非常高。普通CPU可以在100毫秒内找到上千个节点的最大流量。不难发现，对于大额支付，我们可以通过最大流算法得到两个节点之间最大可能的支付金额。如果支付金额小于此金额，我们将通过最大流算法建立支付方案。2基于信标节点的路由协议基于地标节点的路由协议的总体思路如下。首先，每个节点都有资格成为信标节点，每个节点都有权选择哪些信标节点来协助路由。这个前提基本保证了路由方案的去中心化不会被打破。然后，为了提供一定的隐私量，增加支付成功的概率，将每个支付量分成若干部分，每部分在不同信标节点的辅助下进行传输。对于没有碎片的情况，我们认为。灯塔根据自己的视觉为这个量安排一个通道来辅助传输，并通过与这些通道上的节点通信来获得可以通过这个通道的最大量。

早期方法

基于Landmark的路由协议来源于对计算机网络的研究。常见组件如下。熟悉在双向BFS中寻找最短路径的算法的读者知道，在没有权重的有向图上，来自单个源的呼吸优先搜索(BFS)序列的性质保证了从BFS树中的每个节点到源节点的路径，即从节点到源节点的最短路径或最短路径之一。每个界标节点维护两个以自身为源节点的BFS树，一个基于脉冲耦合网络图，另一个基于脉冲耦合网络图，所有通道反向。当然，对于无向图，这两棵树是相同的。因此，对于从到的路径，首先在中找到到达地标节点的路径，然后在中找到到达地标节点的路径。这两条路径拼接在一起，得到从到的最短路径。

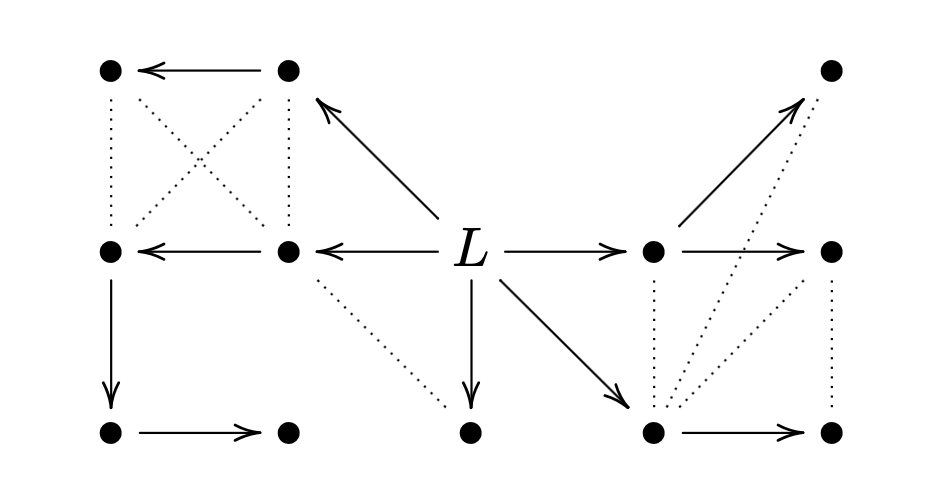
基于树的图形嵌入允许每个灯塔节点将视图中的所有节点视为一棵树，树的每条边对应一个支付通道。这样，从根节点到节点的路径号可以以类似于Trie树的方式用于每个节点。比如下图，节点的标签是，节点的标签是，节点的标签是。当然，我们只是以二叉树为例。实际上，它是一个多树，编码范围不再介于和之间。对于树，编码范围变为。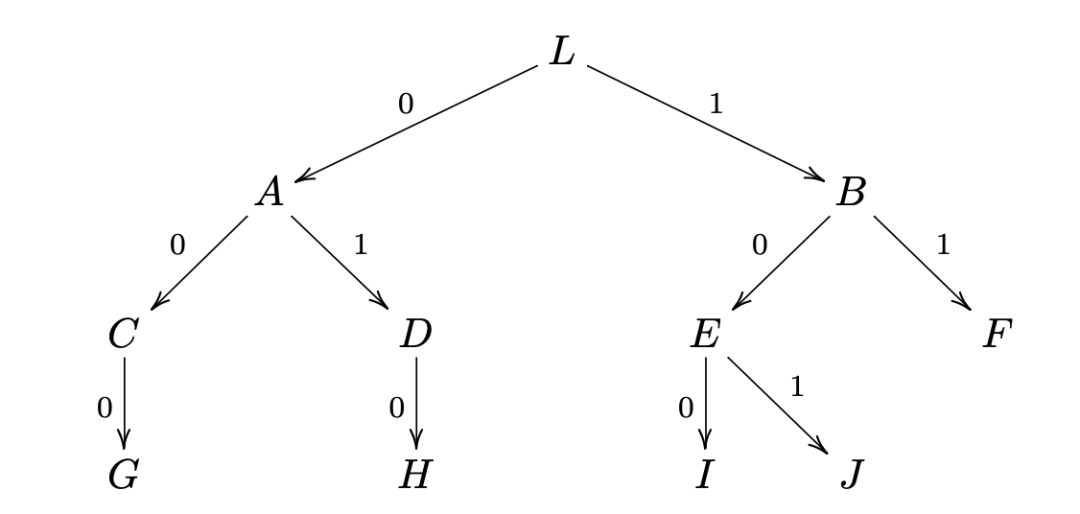

利用这种编码方法，可以有效地确定两个节点之间的路径——，即从支付节点到两个节点的最近共同祖先(LCA)的唯一路径。

SilentWhispers与SpeedyMurmurs

silent耳语的协议本身没有考虑支付网络的动态性，文中的方案也没有考虑配额分片，所以一次支付只使用信标节点。当然，该方案可以扩展到碎片支付方案，但是该方案的通信复杂度随着用于支付的信标节点数量的平方而线性增加。假设您需要处理从到的付款，总金额为。付款人将付款金额分成若干部分，第一部分的路线由协助完成。对于每个():

首先，找到往返于双向BFS的最短路径，

然后通过与路径上各个节点的通信，确定可以通过这条路径的支付金额的大小，即这条路径上的最小保证金。这一步可以通过安全多方计算(MPC)来完成，以确保隐私。

SpeedyMurmurs直接采用了分期付款的方案。此外，与无声说话人的一大区别是SpeedyMurmurs中的灯塔节点通过嵌入基于树的图来提供支付路径，其针对的是无声说话人(1)在动态网络环境下难以维护双向BFS树，(2)即使拓扑距离非常接近的两个节点之间的路由也必须经过Landmark节点，(3)并发性差。每个Landmark根据已有的支付渠道，维护一个以自己为根节点的叉树。并维护每个视场中的节点数。假设您需要使用灯塔节点()处理从到的付款，总金额为。付款人将付款金额分成若干部分，第一部分的路线由协助完成。对于每个()，由两个节点的编号找到的树到树的路径完成相应的支付。3基于数据网络方法的路由协议，因为上述路由方案没有充分考虑实际支付网络的动态性。因此，一些以计算机网络为背景的学者提出了几种将数据网络中的路由方法直接应用于支付网络的方案。由于数据网络的路由理论在计算机网络领域已经非常成熟，这种方案具有很高的可靠性。动态也为这种方案提供了相当大的效率。最经典的是Spider协议。

Spider将支付网络比作数据传输层，采用数据网络的方法进行动态路由。为了匹配数据网络模型，在这个方案中，我们仍然假设所有通道都是双向的。类似于数据网络中的数据包，每个事务被分成几个数据包，并通过不同的路径进行路由。每个金额包都是通过支付网络渠道直接传输，最终到达收款人，转发过程中的节点锁定对应的金额。路由完成后，根据每个金额包的转发路径完成最终支付。

然而，支付网络和数据网络的一大区别在于流量限制的存在。因此，每个通道将对应于一个待定列表，以保存所有尚未以当前吞吐量传输的数据包。只有当有足够的流量从通道的另一端传来(相当于这个方向的裕量增加)时，这个队列中的钱包才能继续传输。值得注意的是，虽然我们用一个量包的传输过程来描述动态路由过程，但其本质是一个路由和锁定的过程。如果不添加，这个路由过程会被误认为是支付过程。4混合路由协议通过对Ripple和比特币支付网络的实际分析，最新研究(在Flash的论文中)发现：

支付网络需要支持大额交易(已被质疑)；

大的交易需要更注重支付的成功率，小的交易更注重效率。

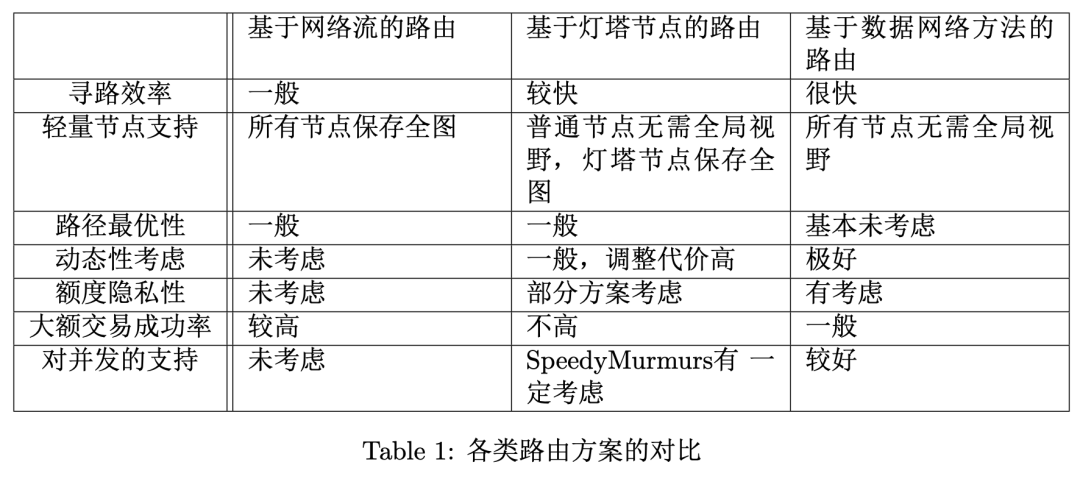
基于这一发现，Flash协议使用基于最大流的路由方案完成大额支付，使用基于数据网络的路由方式进行小额支付。因此，大额交易的支付成功率和小额交易的效率可以得到平衡。

各类路由方案的对比与分析

作者在上面的表1中列出了各种非混合路由协议的优缺点。因为难以量化，所以带有一定的主观色彩。5未来研究展望接下来，笔者提出了一些研究展望，并在本文的最后提出了这一领域的科研可能遇到的问题。

熟悉“基于增广路径的最大流算法”的朋友应该知道，这种算法需要给每条边配备一个“反向边”来描述一个算法中使用的回流。而我们可以惊讶地发现，这种回流恰恰描述了双向支付渠道中从另一个方向抵消的金额。所以增广路径定理保证了即使支付网络不规则地“增广”，任何不超过最大流量的支付最终都会完成。因此，我们得到了一个完全“动态”的基于最大流的路由算法。这一点在现有文献中似乎没有提及。当然，对于绝大多数的小交易来说，用这个算法杀鸡用牛刀都不为过。但笔者认为，这种想法对于早期支付网络中遇到的巨额交易将是有用的。

可以用“最小费用最大流”代替底部最大流，使算法在有多个选项的情况下，选出一组长度最短、总费用最少的路径方案。学过“最小成本最大流量”算法的朋友，此时应该能理解作者的寓意，这里就不展开了。

通过重构支付网络相关的智能合同码或建立替代地标节点，对参与节点进行“引导”构建边缘，从而系统地改善网络的拓扑结构。我对各种界标可能导致的结构做了大量的想象，包括基于超立方体的，以界标为根的平衡树，以界标为根的联截树等等。

如果你想在这个方向上做进一步的研究(支付网络中的路由问题)，特别是如果你的目标是缩短平均跳数，那么可能会出现两大问题：第一个问题是，目前的支付方案在目前的支付网络规模上做得很好。根据SpeedyMurmurs论文中的实验数据，在Ripple网络全盛时期可以达到2到4跳的平均跳数。我们如何在此基础上进行优化？在未来数百万、数亿的支付网络中，更美观、能取得更好效果的算法，在目前的支付网络下，由于其“常数”较大，未必能取得更好的效果。当然，基础研究应该面向大规模支付网络的未来，但是面向未来的研究需要在大规模网络上模拟才能有可信度。接下来，作者解释了如何模拟大规模支付网络的拓扑结构是不可能的。第二个问题是难以进行合理的模拟实验。首先，实事求是的说，目前现实网络的参与者大部分还是少数极客精英和资本，他们的拓扑结构肯定和未来的现实网络有很大的不同。其次，作者认为社交网络中的一些模型不能真实反映支付网络的未来拓扑结构。比如，作者不认为社交网络中常用的瓦特图可以很好地描述未来的网络，因为大多数节点不会建立很多边来使图的密度达到小世界现象的阈值，瓦特图的大前提也就不成立了。综上所述，作者认为对未来支付网络的拓扑结构的研究在今天是非常重要的，也是进一步研究和开发一些支付网络的大前提。