格子的历史

长久以来，数学家们一直在研究格。代表人物有拉格朗日、高斯、闵可夫斯基等。近几十年来，格在密码学、通信和密码分析中有着巨大的应用价值，是一个非常热门的领域。

现代晶格时间轴：

1982年：LLL基归约定理

使用格进行密码分析

1996年：Ajtai-Dwork

首次将格中平均情况和最坏情况的复杂性联系起来

提出了由格构造的单向函数和CRHF函数

2002:发现了平均情况/最坏情况复杂性之间的关系，并且基于格的协议变得更加有效

2005年：雷格夫提出了LWE，并发现了它的量子阻力

提出了PKE、IBE、安倍、FHE等的可能性

什么是格子

格可以被认为是空间中许多规则分布的离散点。

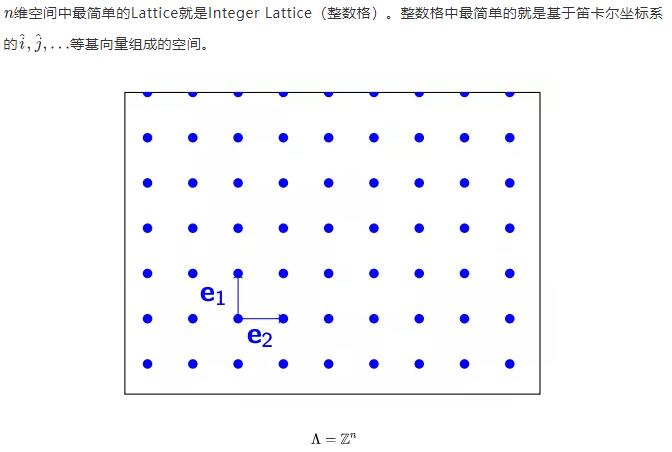
我们可以在这个格上做任何线性变换，然后我们可以得到一个新的格。

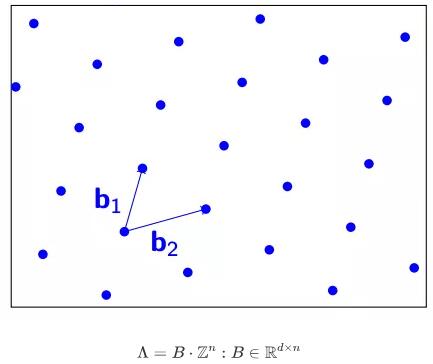
晶格和基底(晶格和基底)

描述一个格的更好的方法是使用基向量。

同样地，我们可以利用线性代数中学习到的基的变化，为这个格找到一组新的基。

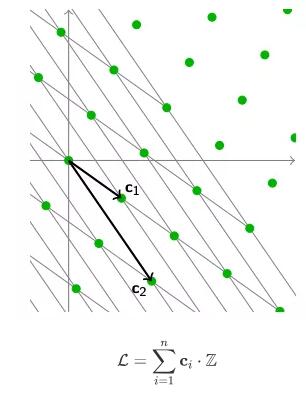
如果我们系统地定义格，我们可以说格是Rn空间中的离散可加子群。

格的基本属性

同样，格的行列式也是由对应于——的基向量组成的同一个平行六面体体积。

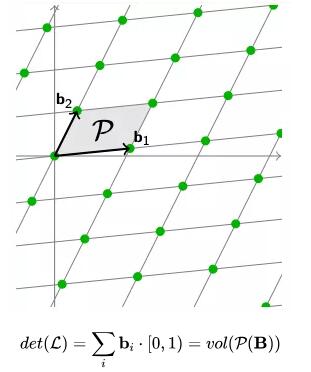
同样，我们改变一组基向量，我们也可以计算它的行列式。

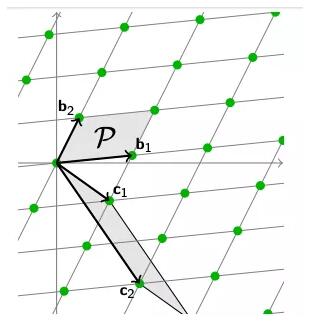
值得注意的是，无论我们如何改变基向量，行列式的大小，即由基向量组成的多面体的体积，是相同的。给定任意一组基向量，我们可以有效地找到格空间的行列式。

晶格密度

我们可以用格的行列式来度量这个格的格分布密度。

首先，我们将由基础向量的最后一部分组成的多面体的中心移动到原点。这样，空间p仍然保持相同的体积。

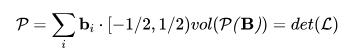
然后，我们可以制作这个多面体的多个副本，然后把它翻译成格子中的每个点。这样，我们将得到p的许多副本，这些多面体可以平均划分整个多维空间Rn。

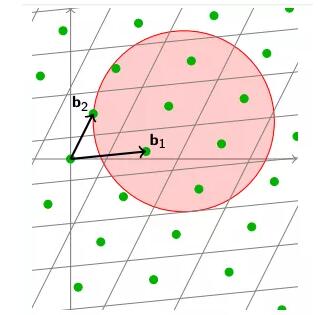
这时，如果我们在这个空间中任意画一个球(多维空间是超球)，那么我们就可以算出这个球覆盖了格中的多少个点。点数等于球体的体积，也就是晶格的密度。

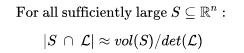
这个概念也很容易理解。我们球体中格点的数量与球体体积中多面体的数量大致相同。

直线

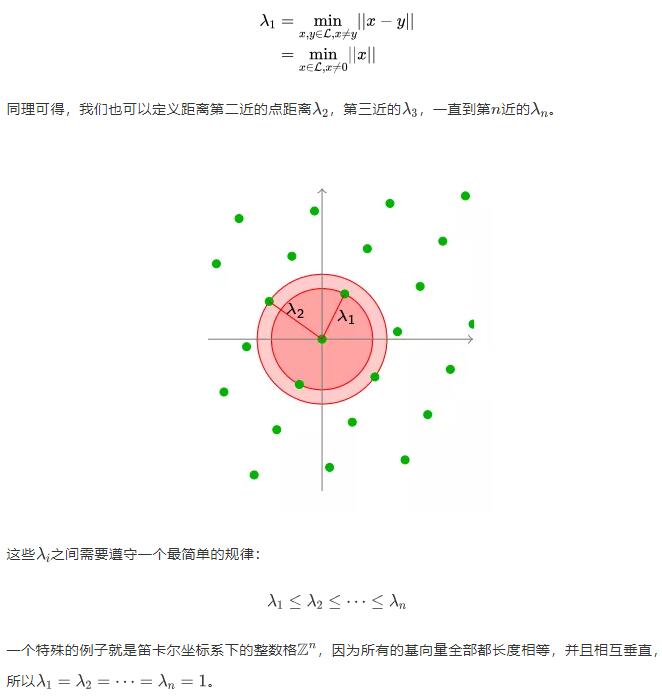
距离函数和覆盖半径

给定任意点t(该点不需要在格子上)，我们可以将距离函数u(t，L)定义为从该点到附近格子点的最短距离。

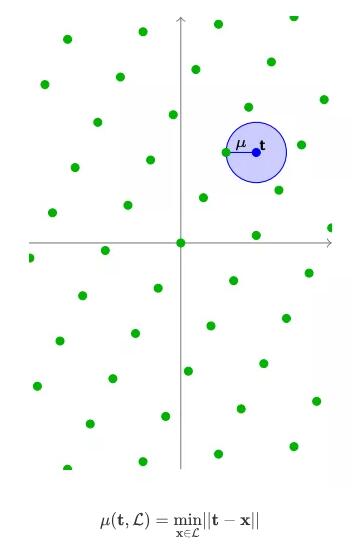
用同样的方法，我们也可以左右移动t的位置，然后我们可以找到在这个格子中能得到的最大u。我们通常称这个最大值为覆盖半径。

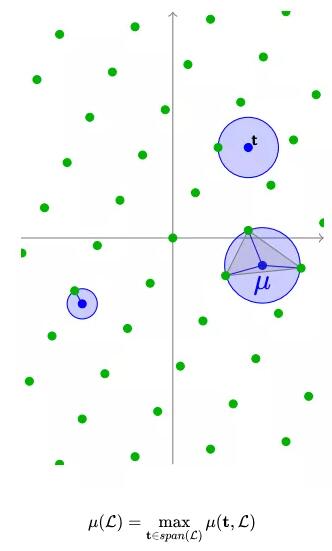
为什么这个最远的距离叫做覆盖半径？这其实很简单。我们可以假设在这个格子中，许多歌曲圆圈是以每个格子为中心画的。

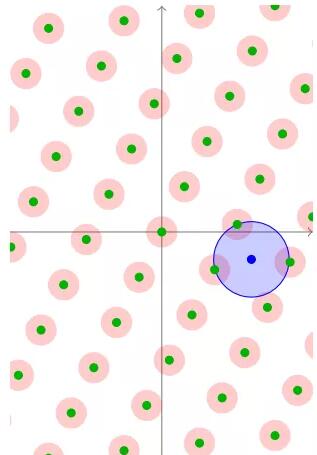
如果圆的半径逐渐扩大，那么所有的圆将逐渐开始覆盖整个Rn空间。

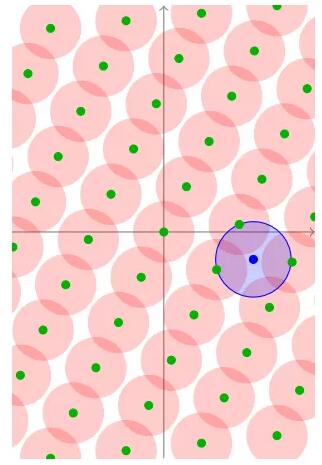
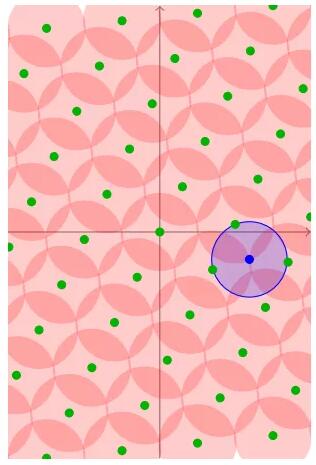
直到所有的圆完全覆盖所有的空间，此时的半径是我们之前得到的u。这是覆盖半径名称的来源。

晶格的光滑性

如果我们稍微改变上述覆盖圆的概念，假设我们不是在每个网格点上叠加一个圆，而是叠加一个随机噪声，其值在圆的范围内，那么当圆的半径达到覆盖半径时，网格本身将与其后面的连续空间Rn合并。

然而，如果仅在覆盖半径上，可以在图上发现，由于网格点之间的相互位置，噪声覆盖的分布非常不均匀。也就是说，叠加噪声后，Rn上的值分布不均匀。

如果我们想使价值的分布更均匀，我们需要更平滑。)格，即继续扩大圆的半径。理论上，当半径接近无穷大时，我们得到的分布是最完美和平均的。然而，当圆是无限的时候，这种构造就没有实际意义了。

所以一般来说，我们将给出平滑半径的最大上限。最大上限由该格中距离最大的最短向量决定。因为当我们的半径大于最短向量时，圆会覆盖太多的点(因为最短的距离决定了点之间的距离)，然后构造就失去了意义。

闵可夫斯基凸集定理(凸体定理)

对于格，闵可夫斯基给出了一些有趣的定理。第一个定理用于寻找格点周围最近的其他格点，即凸集定理。

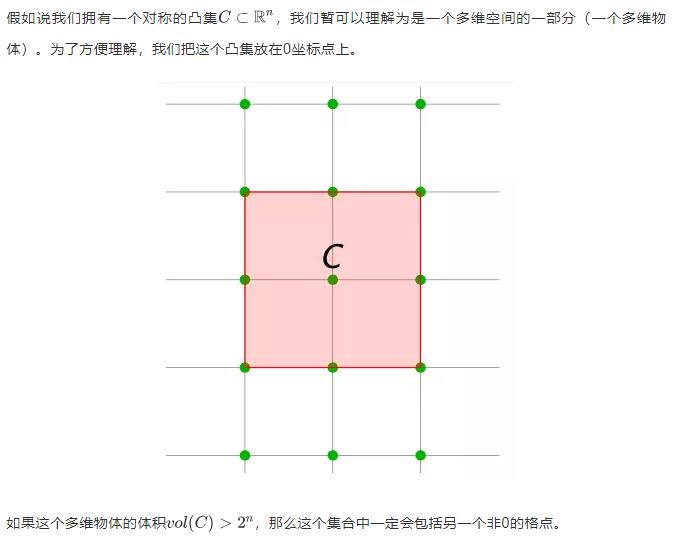
众所周知，在整数格Zn中，由于从原点到所有下一个点的距离形成的空间正好是2n，所以任何凸集(集的表面不能有凹陷)只要其体积大于2n，就会溢出这个空间，然后覆盖一个非零格。鸽子洞原理可以形象地理解它。

下一步，如果我们用一个不规则的格来代替它，也就是说，把线性变换叠加在原来的锌上，这个定理仍然成立。

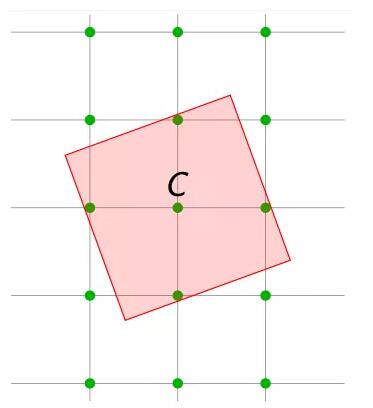
闵可夫斯基第二定理