概述概述

观点一：2019年7月13日至2020年7月13日，数字现金市值前十名的整体风险水平下限比a股市值前十名高24.52%

观点2:就超额回报而言，a股前十名股票组成的投资组合高于数字现金前十名股票组成的投资组合(夏普比率1.89比1.67)。然而，就绝对回报而言，a股投资组合低于数字现金投资组合(回报率为39.76%对114.87%)

报告报告

在介绍研究成果之前，首先对本文使用的模型进行了总结。

马科维茨模型

对于任何投资者或股市投机者来说，首先要考虑的是投资回报和相关风险。毕竟，世界上没有免费的午餐，这意味着没有初始投资，钱不可能凭空而来。同样，你不能在没有风险的情况下赚钱，所以风险随着有效边界上证券的预期利润而增加。根据现代投资组合理论(MPT)，为了建立最优投资组合，采用了基于收益率、风险和证券相关性的统计考虑的选择方法。证券可以是股票、债券、指数、期货/期权、结构性产品、商品和货币；几乎任何能够在预定时间范围内准确确定回报率的交易资产。

投资组合资产的多样化旨在降低特定发行人或市场的非系统性风险。然而，在哈里马科维茨(Harry Markowitz)于1952年在他的文章《投资组合选择》中发表现代投资组合理论之前，投资者在建立投资组合时就已经注意到了对单个证券的风险和收益的评估。投资决策的基础是确定回报最高、风险最小的证券，然后将它们放入投资组合。马科维茨提出了另一种投资多元化的方法，即在评估投资组合的整体风险后建立投资组合，即选择整体投资组合，而不是建立由不同的预选证券组成的投资组合。因此，重点在于资产特征之间的关系，而不是实际特征。

1990年，哈里马科维茨、莫顿米勒和威廉夏普因其在投资组合理论方面的工作获得了诺贝尔经济学奖。其基本假设是，一段时间内的回报证券是随机变量，因此可以计算出数学期望和标准差，因为标准差被认为是投资风险的度量。投资组合E(rP)的预期回报率是其中包含的资产的预期回报率的线性组合，这些因素是资产在投资组合中的相对份额。投资风险用标准差(标准差)来衡量，标准差取决于单一资产收益率的非线性标准差和协方差。

马科维茨的多样化思想是，随着资产越来越多，相应的协方差量明显大于资产量，因此投资组合的风险将在更大程度上取决于资产之间的协方差，而不是单个资产的风险。马科维茨模型参数优化的表观形式有以下数学表达式：

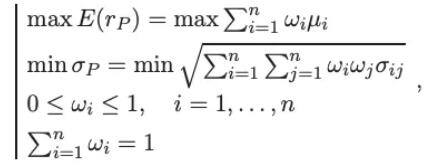
I是投资于I的资本比例；Ri是资产I的收益率；I是资产的预期回报率；其中ij是资产I和j的收益的协方差；E(rP)是投资组合的预期回报率。P是投资组合的风险。

这种模型对于大多数实际情况来说足够普遍，对于理论分析和数值求解来说足够简单。该模型以其创始人马克维茨模型命名，但也以均值-方差模型的形式出现。Markowitz模型是基于投资者和金融市场行为的几个假设之上的。36366.44444444461

-投资者可以估计某个持有期内可能的回报概率分布。

-投资者具有单周期效用函数，它在财富边际效用递减的框架内最大化效用。

-投资者利用可能的回报值的可变性来衡量风险。

-投资者只关心他们的投资组合在特定时期的回报率的平均值和方差。

-投资者使用的预期回报和风险通过回报概率分布的前两个时刻来衡量

-期望值和方差。

金融市场没有摩擦。

-没有交易成本或税收。

投资组合有效边界

每一个可能的投资组合都可以在风险回报空间中绘制，所有这些可能的投资组合的集合定义了这个空间中的一个区域。这个区域的上边缘被称为有效边界，有时被称为“马科维茨子弹”。沿着这条线的投资组合代表在给定回报水平下风险最低的投资组合(明确排除无风险期权)。相反，对于给定的风险，有效边界上的投资组合代表了提供最佳可能回报的投资组合。从数学上讲，有效边界是风险最小的组合和收益最大的组合的交集。

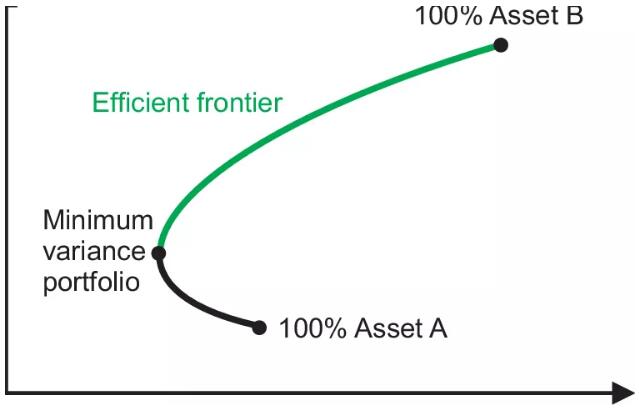
上图显示了整个投资机会集，即由不同比例的资产组成的投资组合所能提供的所有可实现的风险和回报组合。在有效边界上提取的投资组合中特定风险资产的组合代表了在预期回报水平下的最低可能风险或在可接受风险水平下的最佳可能预期回报。

结果分析与讨论

一般来说，对股票的风险和预期回报做出一个有用的、现实的预测至少需要30年。不幸的是，桶效应决定了这个缺点在于数字现金没有这么长的历史。本研究的数据仅包括按市值计算的前10只股票的365天历史价格，而a股市场前10只股票的365天历史价格。具体而言，从2019年7月13日至2020年7月13日，将跟踪每日股票收盘价。截至2020年7月，这两个市场的十大市值目标如下：

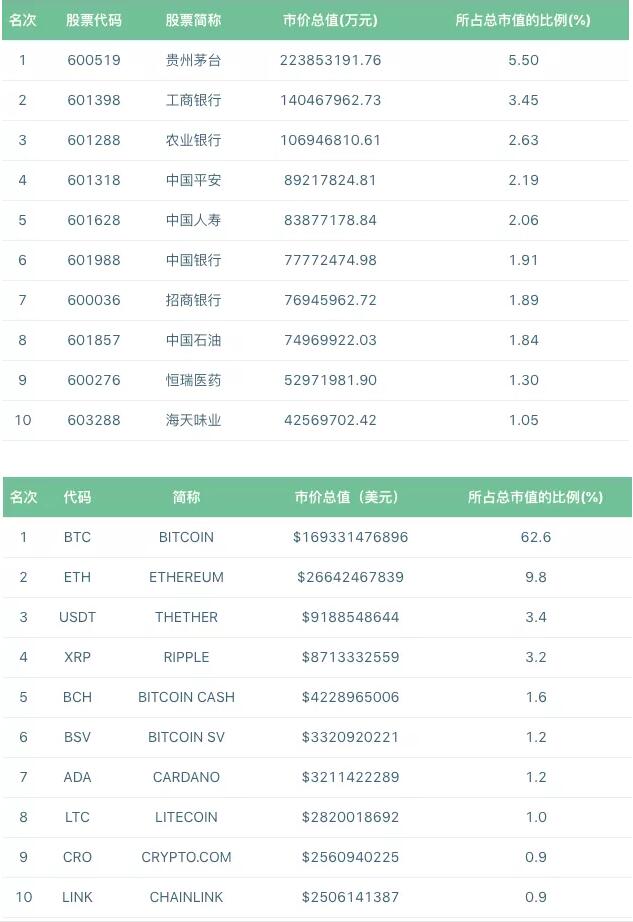
选定股票的风险和回报

我们可以计算20种资产的平均周回报率。在2019年7月13日至2020年7月13日的研究期间，20个样本中有10个产生了正回报。剩下的6%表现不佳，回报率为负。

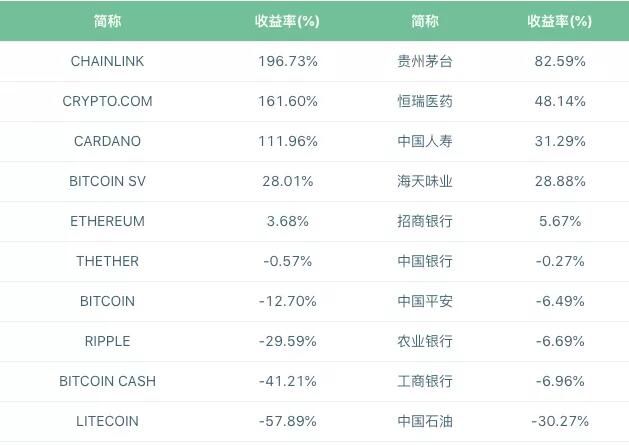
上表列出了十大股票和十大数字现金的回报率比较。从表中可以看出，在所有投资产品中，数字现金链链接的收入最高。数字现金的前三名收益率远高于a股。

最小化投资组合风险的有效边界

以下两个图中所示的有效边界说明了在任何目标回报率下具有最低风险的一组有效组合。在相同的回报水平下，没有其他投资组合的风险低于位于该有效边界的投资组合的风险。

我们用这10只股票的不同比率做了100万个随机假设，并以每个假设的收益率作为x轴和y轴坐标做了一个散点图。此外，我们根据每个组合的夏普比率将颜色从低到高和从红到绿进行设置。

数字现金组合

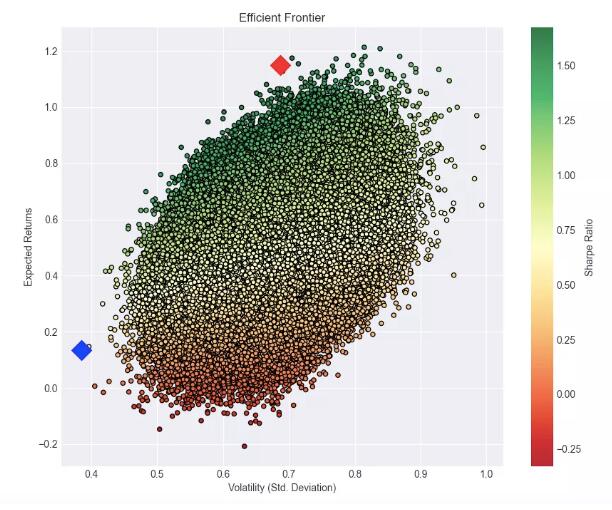
股票投资组合

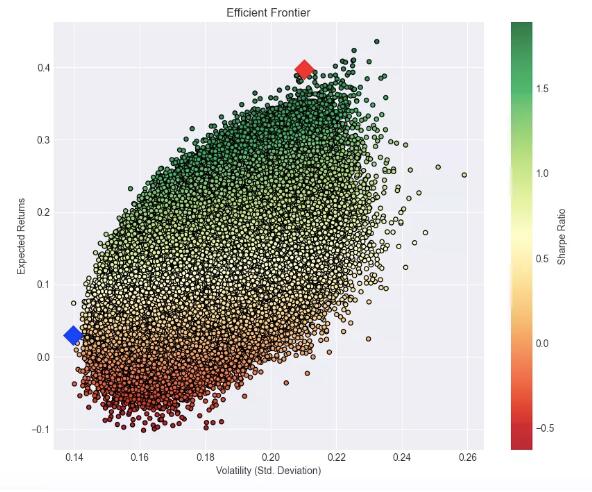
一旦构建了有效边界，特定投资者的任务就是根据他们独特的风险偏好从图上的点中选择他们自己合适的投资组合。风险容忍度低的投资者倾向于选择风险回报组合在边界左侧的投资组合。相反，那些愿意接受高风险以赚取更多回报的人可能会对位于边界右侧的投资组合感兴趣。

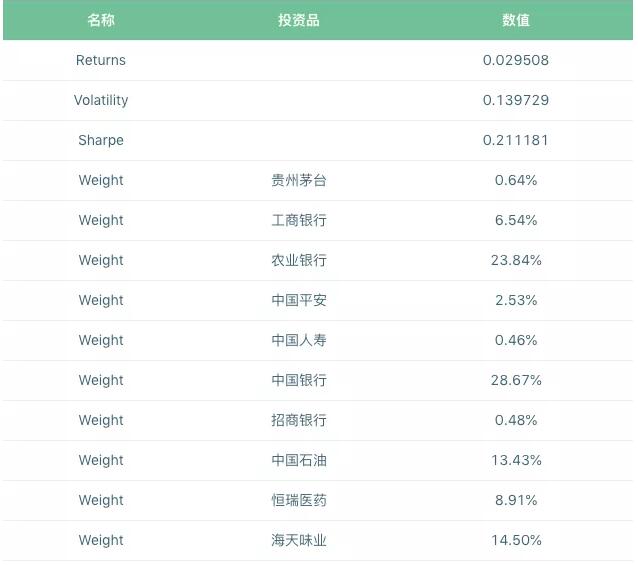
最小风险组合

根据markowitz模型的定义，我们得到了最小风险投资组合中每个组成资产的准确权重，如下图所示。在这个投资组合中，10个股票样本的资产比例分布仍然存在差异。值得注意的是，收益率最高的贵州茅台和恒瑞药业的分配比例不高，分别占投资组合总额的0.64%和8.91%。中国银行和农业银行的权重分布最大，分别占28.67%和23.84%，收益率分别为-0.27%和-6.69%。最小风险投资组合的平均回报率为2.95%，风险水平为13%。这个投资组合的夏普比率是0.211。

股票投资组合

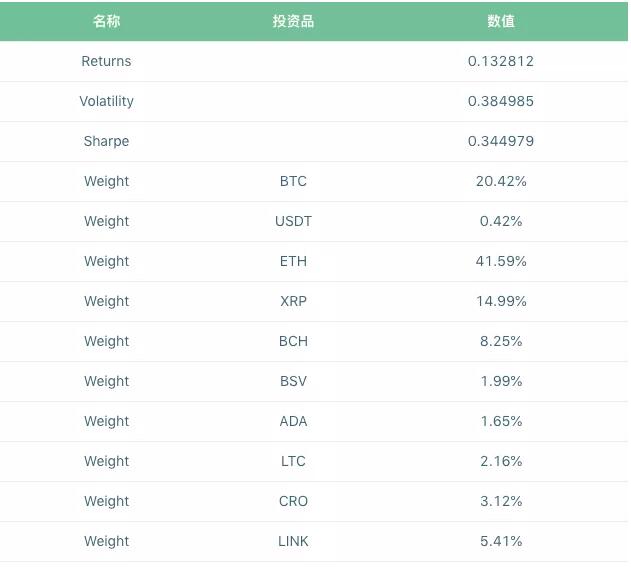
在下面显示的数字现金投资组合中，10个数字现金样本的资产比例分布仍然存在差异。值得注意的是，收益率最高的沪港通和CRYPTO.COM的配股比例仍然不高，分别占总投资组合的5.41%和3.12%。ETH和BTC的权重分布最大，分别占41.59%和20.42%，收益率分别为3.68%和-12.7%。最低风险投资组合的平均回报率为13.28%，风险水平为38.50%。这个投资组合的夏普比率是0.34。

最大夏普比率投资组合

除了最小风险投资组合之外，我们还计算了最大夏普比投资组合中每种成分股票的准确权重，如下表所示。在最大夏普比率投资组合中，资产仍然保持不同的权重分配。10只股票的配置差异很大。值得注意的是，贵州茅台和恒瑞药业是权重分配最大的股票，分别为30.04%和26.90%。该投资组合的预期收益率为39.75%，风险水平为21.01%，夏普比率为1.89。

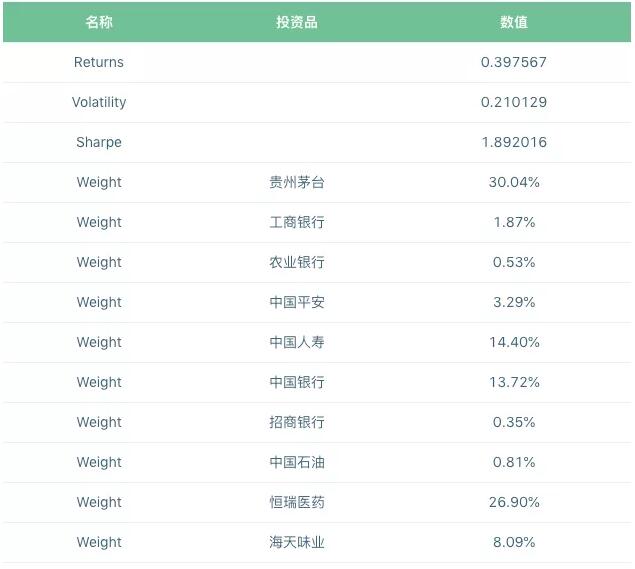
如下表所示。在最大夏普比率投资组合中，在最大夏普比率投资组合中，资产仍然保持不同的权重分配。10种货币的配置差异很大。值得注意的是，link和cro是权重分配最大的股票，分别为30.61%和32.92%。该投资组合的预期收益率为114.87%，风险水平为68.64%，夏普比率为1.67。

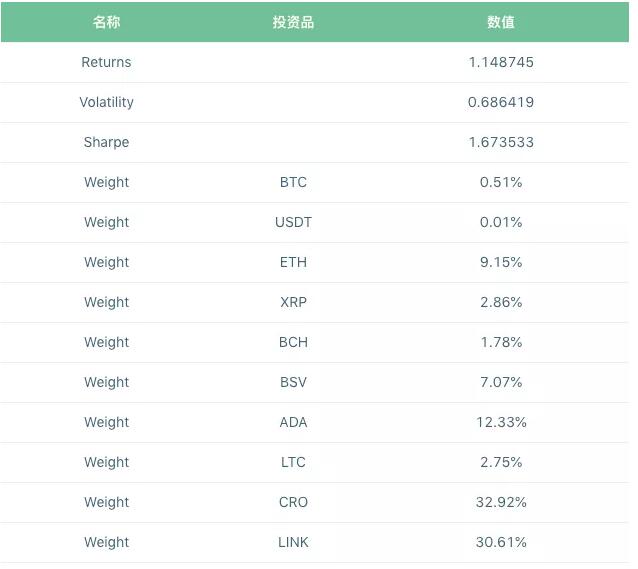
结论

在本研究中，达到了用马尔可夫模型建立最优投资组合的目的。通过投资位于有效边界上的有效投资组合——，投资者可以在一定的风险水平、最大夏普比率或最小风险下获得最大的投资回报。这就是马科维茨的多元化力量。如果投资者知道如何恰当地运用马科维茨模型，他们就能提高自己的投资业绩。