在加密区块链数据库系列的第二部分，我们将介绍在区块链存储动态加密的多幅地图(EMM)的三种方案，每种方案在查询、添加和删除效率之间实现不同的权衡。

基于列表的方案基于列表的方案(LSX)

回想一下，多重映射是多个标签/值元组的集合。在这个结构中，我们将与每个标签相关联的值存储在区块链的一个单独的逻辑链表中。但是，为了确保机密性，我们会在将前一个地址添加到正确的链接列表之前对其进行加密。准确地说，给定元组(v1，vn)要添加到标记l，我们为每个I1，n]添加EncK(vi || ri-1)到区块链。对于第一个值，ri-1是l链表当前头的地址。为了实现动态性，我们使用了延迟删除，即所有添加和删除的值都标记为add()或delete (-)，只有在查询过程中从输出中删除标记为delete的值，才能执行删除。有关LSX的解释，请参见图1为清晰起见，我们在图中省略了值和地址的加密。

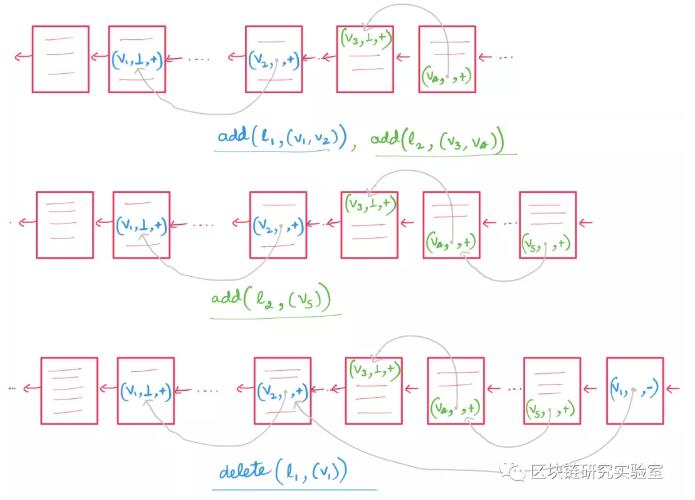
效率：很容易看出，LSX在添加和删除方面有最好的时间复杂度：对于每个操作，我们只写与元组大小一样多的值。然而，它的查询复杂度在更新数量上是线性的。特别是，在每个查询中，我们读取所有添加或删除的值。如果所有的更新操作都是加法操作，该方案具有最佳的查询复杂度，但是如果大多数更新是删除操作，该方案将产生大量的查询开销。这种方案的另一个缺点是，添加和删除操作都需要用户和区块链之间的线性写轮数(就元组大小而言)。这是因为在计算vi-1的地址之前，值vi不能被写入，所以每个值必须在单独的写入轮数中写入。

计算写轮数非常重要，因为由于挖掘和稳定性的原因，区块链的写操作比区块链的读操作耗时更长。因此，尽可能并行化写入非常重要。我们将这一指标称为稳定复杂性，因为写入所需时间取决于交易稳定性所需时间——例如，对于比特币，写入时间可能高达60分钟(最长链中的一个块必须达到至少6个块才能成为不可变的)。

接下来，我们描述了一个基于树的方案，它将稳定性复杂度从线性提高到对数。

基于树的方案(X)

在这个方案中，我们修改了值的组织，以便在存储值之前减少所需的地址数量。给定要添加/删除的元组，我们覆盖完整的二叉树，而不是链上的链表。这使我们能够在树的相同深度并行插入所有值。此外，我们将跨多个添加/删除操作构建的树的根链接起来。请注意，这种简单的结构变化将稳定性复杂性从线性降低到对数。

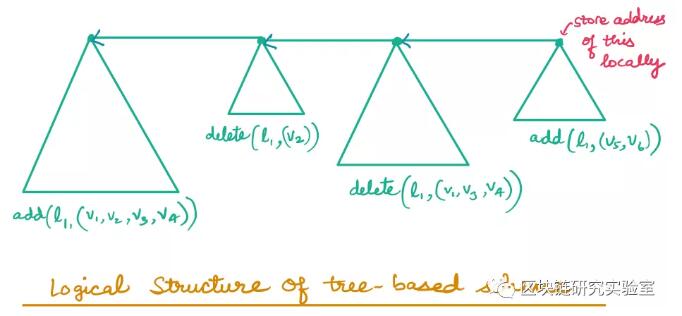
由于上述两种方案的查询复杂度与添加/删除的值的数量成线性关系(当大多数更新是删除操作时，这可能是非常糟糕的)，我们现在将描述一种将查询复杂度提高到最佳的方案，但是删除的成本有点昂贵。

基于块的方案基于补丁的方案

注意，LSX的查询复杂度不是最优的，因为当遍历链表1时我们不知道被删除的值，所以我们最终读取所有的值，不管它们是否被删除。为了解决这个问题，我们在链接列表的顶部附加了一个额外的数据结构(称为块)。块程序是允许查询算法跳过已删除值的地址对。例如，假设我们有以下链接列表：

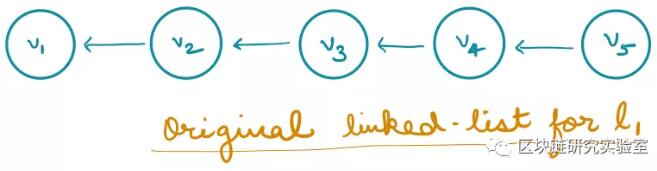
当删除v2时，我们创建一个块(addr(v3)addr(v1))，当删除v4时，我们创建另一个块(addr(v5)addr(v3))。目前，我们不需要担心在哪里和如何存储块。然而，给定这些块，查询算法可以容易地跳过删除的值v2和v4:从v5，它将使用第二个块跳转到v3，从v3，它将使用第一个块跳转到v1。

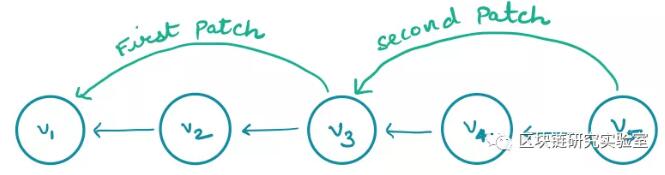
现在假设v3也被删除了。在这种情况下，我们将创建一个新的块(addr(v5)addr(v1))，这可以帮助查询算法跳过所有值v2、v3和v4。

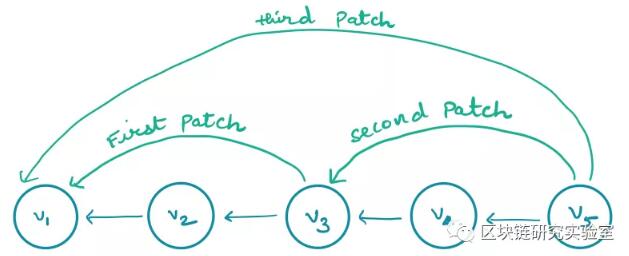
有两个问题：

1.V5中有两个块：一个进入v3，另一个进入v1。为了使查询正确跳过已删除的值，应该使用(v5v1)而不是(v5v3)。

2.块的数量等于删除的值的数量，这意味着搜索块与使用延迟删除一样昂贵。

为了解决这个问题，我们需要确保清理(或删除)旧的块。确切地说，在删除v3之后，我们应该同时删除(v5v3)和(v3v1)。(v5v3)的删除确保了正确性，而(v3v1)的删除确保了效率，因为剩余颜色块的数量最多是未删除值的数量。

块数据结构：因为块的数量可能很大，它们不能存储在本地，但也必须存储在区块链。我们可以在链表或树中组织块。不管我们决定什么，我们称之为块结构。请注意，无论我们如何组织区块链的块结构，从其中删除块的要求都会带来鸡和蛋的问题：从链表中删除多图值需要从块结构中删除块。那么我们应该修复街区结构吗？

我们使用另一种叫做“写和复制”的技术来解决这个问题。在高层次上，这种技术复制“节点”，并修改副本，而不是修改原始节点。让我们用一个例子来解释。假设我们将块结构表示为链表。此外，假设在100的区块结构中有100个区块。

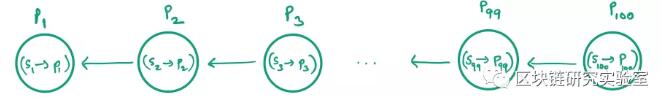
要删除P2，我们需要将P3指向P1。然而，因为P3存储在区块链，所以不能将其更改为指向P1。因此，我们创建了P3的一个副本P3，以便它存储与P3相同的块数据，并指向P1。然而，这要求P4指向副本P3，这是不可能的，因为它也存储在区块链。因此，创建了P4的副本P4。这个过程将扩展到链表的头部，从P3到P100的每个节点都将被它的副本所取代。

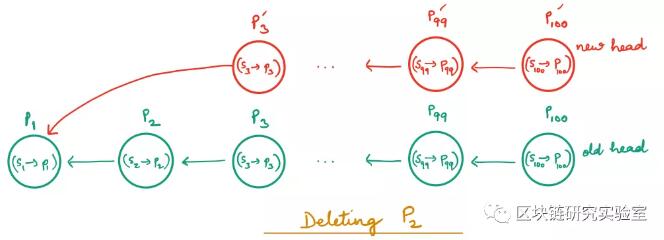
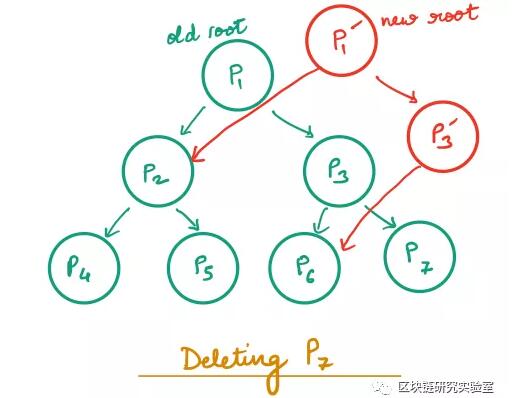
显然，这是非常昂贵的：删除块结构的链接列表中的深层块将触发所有后续块的重写。因此，我们将块结构表示为平衡二叉树。在这种情况下，删除一个块只会触发创建与树高相同数量的块。

效率：让| MM [l] |是多重映射中当前与标签l相关联的值的数量。换句话说，| MM [l] |代表l的未删除值的数量。我们在这里不进行讨论，但是不难发现块结构中的最大块数量是| MM [l] |。由于查询算法现在可以通过使用块来跳过删除的值，并且搜索块的成本不高，所以查询时间复杂度为O(| MM [l] |)，这是最好的。加法的复杂度和以前一样，所以也是最好的。删除复杂度为O(| v | log | MM [l] |)，其中| v |是要删除的值的数量。这是因为对于每个被删除的值，一个新的块被插入到块树中和/或它花费(log | MM [l] |)时间来删除旧的块。

稳定性的复杂性：由于加法运算以链表的形式增加值(与LSX相同)，所以加法运算的稳定性复杂性为0(| v |)。然而，删除的稳定复杂性是0(log | MM[l]|)，因为在块树的同一级别上进行的所有修改都可以并行进行。

结论

我们讨论了如何将端到端加密集成到区块链数据库中，更具体地说，讨论了在区块链存储端到端加密多重映射的方法。因为多重映射有足够的表达能力来表示键值存储，所以它提供了一种在区块链上存储键值存储的方法。我们讨论了三种EMM构造，它们实现了查询、添加和删除效率之间的不同权衡。但是有一些有趣的开放式问题。

我们发现，当X的添加/删除时间复杂度最好时，X的查询复杂度较差。另一方面，PAX实现了良好的查询复杂度，但稳定的添加/删除复杂度较差。这就提出了以下自然的问题：我们能设计出一个两全其美的方案吗？

我们还展示了LSX和X都可以使用打包，这允许在单个事务中存储多个元组值。对于允许大型交易的区块链，打包可以提高性能。不幸的是，我们的PAX结构不支持包装，所以一个自然的问题是：我们能给PAX增加包装吗？