这个周末我有空谈谈我对快速傅立叶变换的理解。学习零知识证明的小伙伴理解这一部分很方便。从一开始，零知识就证明Groth16算法是基于QAP问题的：

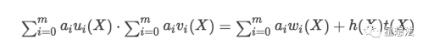
在使用Groth16计算证明之前，需要计算h。目前，快速傅立叶变换算法被广泛使用。

1.快速傅立叶变换计算原理

为了学习快速傅立叶变换的计算原理，我们仍然需要看第三十章(多项式和快速傅立叶变换)的算法介绍。算法介绍，讲述事物，讲述前因后果清晰，逻辑性强，细致入微。本章从多项式的表示开始，多项式可以用两种方式表示：系数表示和点值表示。

系数表示对多项式加法很友好，时间复杂度为O(n)，但多项式乘法不友好，时间复杂度为O(n * 2)乘以多项式的一项。点值表示对多项式乘法友好，时间复杂度为0(n)，但多项式加法不友好。

离散傅立叶变换使用特殊的点来计算该值。这些特殊点是单位根的幂。利用这些特殊的点，系数表示和点值表示之间的关系可以通过快速傅立叶变换来计算。时间复杂度为0。

算法简介该图可以很好地解释这些计算之间的关系：

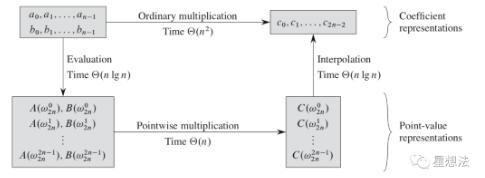
在系数表示的情况下，多项式乘法的计算复杂度为0(n * 2)。如果首先将其转换为点值表示，然后转换为系数表示，则计算复杂度为0(NLO gn)。

n次的单位根

n次有n个单位根。单位根满足w**n=1。

这些单位根有一些性质或定理：

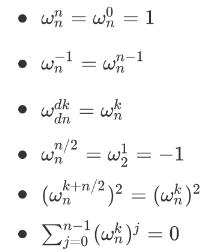
快速傅立叶变换的基本原理

快速傅立叶变换用于计算离散傅立叶变换，时间复杂度为0。原理是将多项式分解成奇数和偶数部分(假设n是2的幂，n不是2的幂，后面有相应的算法):

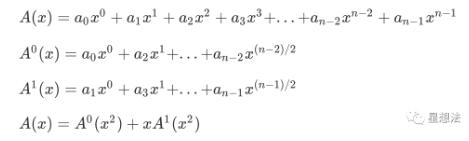
也就是说，计算A(x)的对应值可以分解成两个子多项式(奇偶性)，并且每个多项式的点是前一个多项式的平方。从递归的角度来看，我们可以看到这些子多项式可以进一步划分为更小的多项式。整个计算的复杂性：

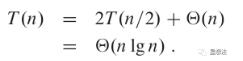
如果输入点也分为两部分，每部分为n/2，k的范围为0~n/2，则为：

这就是传说中的“蝴蝶计算”。在两个子多项式的值的计算完成之后，原始多项式的两个相差n/2的点的值是一加一减去两个子多项式的值。

整个计算算法的伪代码如下：

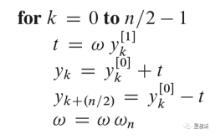
W _ n k，作用于第二子多项式的结果，称为旋转因子。整个蝶式操作可以用直观的图形表示如下：

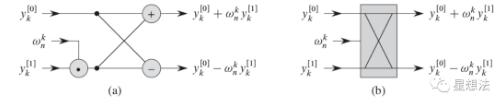
八阶多项式示例

算法介绍清楚地给出了8阶多项式快速傅立叶变换的计算过程：

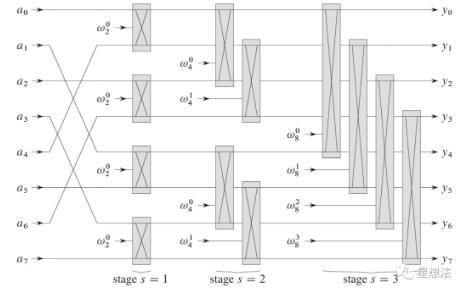
在阶段s=1的情况下，也就是说，在底层的两个一阶多项式被合并。旋转因子为w _ 2 0。注意，该层的输出结果将被用作下一级s=2的输入，并且该层的旋转因子是w _ 4 {0，1}。这一层处理“两个”二阶多项式的组合。在奇偶除法的情况下，第一/第二元素和第三/第四元素(跨度2)进行蝶形运算。依此类推，直到阶段s=3结束。

整个过程可以用Merkle树图像来表示：

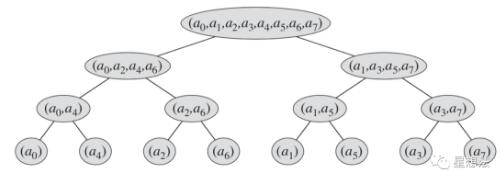
注意最低元素的位置。递归除法不再是连续的。算法介绍还总结了相应的计算方法，感兴趣的合作伙伴可以查看。

你可以回到大脑，体验这个公式：

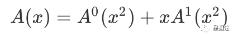
由于特殊的取点原因(w 2等于阶数减半)，次多项式的值也是结果多项式的一半。因为点被分成一半(只是次多项式的阶)，并且因为旋转因子只是正和负，所以存在蝴蝶关系。每一层的子多项式的元素被加倍。

2.快速傅立叶变换通用计算扩展

在理解了两点快速傅立叶变换的计算逻辑后，它可以扩展到一般的计算。推荐另一个网站(注意多项式符号与上面的略有不同):

http://www.bealto.com/gpu-fft2_fft.html

多项式不再分成“奇数”和“偶数”部分，而是分成p个部分，每个部分都有q个元素：

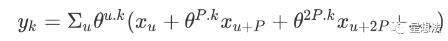
X_u是系数。u的范围是0-P-1。首先，在此划分下定义离散傅立叶变换计算：

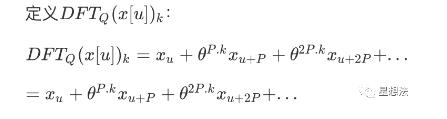
DFT_Q代表Q个元素，x[u]代表Q个元素序列，每个元素序列跨越p，p * q=n。

如果输入也被分成p个部分(就像在等分的情况下把输入分成两个部分)，k可以表示为k=v Qj，v=0.q-1，j=0.p-1。其中DFT_Q (x[u])表示为z[u]。

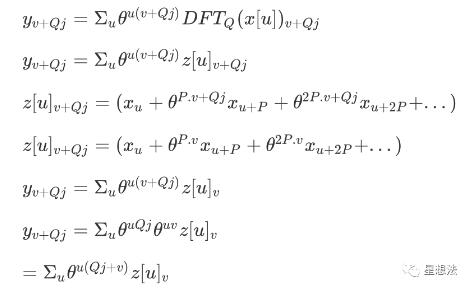
也就是说，当P*Q被分组时，蝶形运算如下：

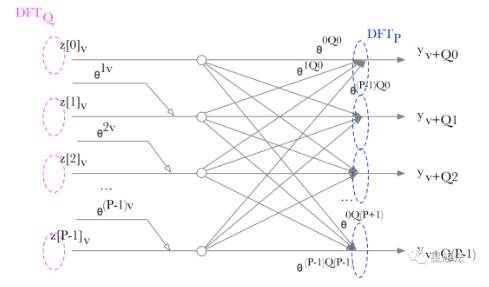
此外，y的每个元素的计算可视为一个新的离散傅立叶变换：

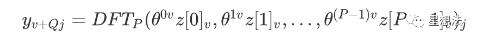
在了解这些的前提下，可以清楚的看到网站给出的P*Q分组计算示意图：

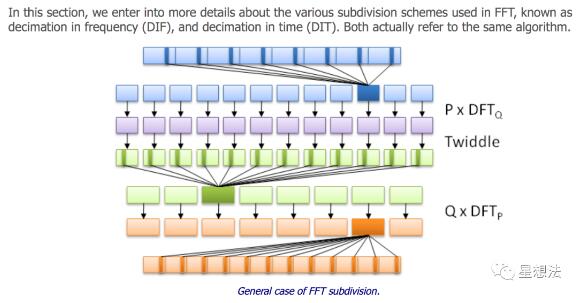
整个快速傅立叶变换计算包括三个部分：

1/P DFT_Q计算(z[0]，z[1]，z[P-1]) 2/乘以旋转3/量子密度泛函理论计算

在q DFT_P计算之后，有必要将P计算数据“分散”到以q为偏移的特定位置。

摘要：

零知识证明，在格罗16的计算中，快速傅立叶变换计算是用来计算h的。快速傅立叶变换的蝶形运算是理解快速傅立叶变换计算的基础。二分法情况下的计算相对清晰，详细的推导过程在算法介绍中给出。P*Q的一般计算和推导比较复杂。