私钥对加密货币的重要性是不言而喻的。在这个世界上，人们总是在考虑破解比特币私钥。

最粗鲁的方式是以详尽的方式与比特币私钥猛烈冲突。大型比特币对撞机（LBC）是一种使用清晰线性强力搜索算法的组织，这种方法在量子计算中不存在。在取得实质性进展之前，可以说是愚蠢的。

对于泄露的公钥，使用平方根离散对数算法是恢复这种短私钥的更有效方法，而宾夕法尼亚大学博士后研究员Joachim Breitner和大学计算机科学与工程学院加州。 Nadia Heninger副教授共同撰写了一项名为《的研究，针对加密货币弱ECDSA签名的格子攻击》。

在这项研究中，我们看到了比特币，以太坊和Ripple区块链，以及HTTPS和SSH中的私钥，它们有几种不安全的用途，所以它们可能会被破解。结果数字不大。在实验中，研究人员计算了300多个比特币私钥（余额约为0.00818975 BTC）和30.40 XRP，但实验告诉我们，我们要正确使用密码货币。这实际上是一个非常棘手的事情。如果你做得不对，你可能会赔钱。

使用ECDSA（椭圆曲线数字签名算法）创建加密签名时，需要提出256位随机数的随机数。每次签名时使用不同的nonce非常重要，否则其他人很容易获得签名并使用相对简单的数学来计算私钥。使用您的私钥，他们可以花掉您所有的比特币。实际上，有证据表明区块链上总有人查看是否存在此类重复的非法，如果检测到，他们将计算相应的私钥并从中提取资金。

没有多少人知道这种类型的攻击，但对于加密社区来说，这并不新鲜。攻击者可以根据不同但类似的随机数来计算私钥：例如，如果它们彼此接近（只有低点不同，或者它们的差异恰好是2的幂（只有高点不同）。这使用了基于格子的强大技术。本文的主要贡献是连接密码学和加密货币，看看是否存在这些漏洞。

事实上，加密货币确实存在这样的漏洞。幸运的是，并不多，但确实存在，并且有多个来源。不幸的是，很难弄清楚是谁制作了这些签名以及使用了什么代码，所以我们只能猜出这些错误的原因。大量受影响的签名与多签名事务有关，因此我们认为硬件令牌可能是导致此问题的原因。

虽然我们不确定导致这些问题的具体实现，但我们仍然可以观察到一些有趣的细节。最好奇的当然是：

一组签名是由攻击者创建的，该攻击者清空泄露密钥的帐户（例如使用弱密码创建或以其他方式泄露到Internet的帐户）。

因此，看起来攻击者已经设置了一个程序来监视区块链，这将清空泄露的帐户。

我们需要担心吗？
 
可能不需要。官方区块链客户在这方面做得很好（至少在这部分），他们使用正确的随机现时，因此作为用户，你不必太担心。事实上，自2016年以来，比特币客户使用了确定性签名（RFC6979）方案，完全消除了流程中随机性的需要。

如果你使用的是非标准库，或者你自己编写了一个密码例程（只有你有充分的理由这样做），那么你应该确保他们使用RFC6979（关于这个主题，而不是钱包） ）该团队在2014年发送了一篇文章《分钟，以了解RFC6979》）。这对嵌入式设备或硬件令牌更为重要，因为很难找到良好的随机源。

以下是该论文的部分翻译：

标题：格式攻击密码证据弱ECDSA签名（格子攻击

作者：Joachim Breitner和Nadia Heninger
机构：DFINITY Foundation，Zug，[电子邮件保护]加州大学圣地亚哥分校，[电子邮件保护]

摘要。在本文中，我们对公共和Internet扫描中包含的数字签名执行密码分析攻击，该攻击计算数百个比特币私钥和数十个以太坊，Ripple，SSH和HTTPS私钥。 ECDSA签名算法需要为每条消息生成秘密随机数。必须以完全相同的方式生成此随机数，否则攻击者可以使用随机数偏差来计算长期签名密钥。我们使用基于格的算法来解决隐藏数量问题，以有效地计算由于多个明显的实现漏洞而与偏向签名随机数一起使用的私有ECDSA密钥。

一，导言
 
ECDSA签名算法的安全性至关重要，依赖于正确生成用作临时私钥的每个签名随机数值。众所周知，如果使用ECDSA私钥对具有相同签名随机数的两个消息进行签名，则长期私钥易于计算。

但是，重复的随机数值不是唯一可以使ECDSA密钥不安全的偏差类型。事实上，如果有足够的签名，ECDSA签名随机数的任何不一致都可以暴露私钥。在本文中，我们对从比特币，以太坊和Ripple区块链以及ssh和https收集的ECDSA签名进行了基于格的密码分析攻击，并有效地计算了数百个比特币私钥和少量以太网和SSH私钥。

此外，我们发现由于重复签名，大量比特币，以太币，Ripple，ssh和https私钥泄露。我们应用的网格攻击是一种基于隐藏数问题的求解算法。虽然隐藏号码问题是许多加密文献中基于侧信道攻击恢复私钥的流行工具，但据我们所知，我们是第一个观察到该技术可以应用于加密货币的人。签名。使用这种技术，我们计算了大约300比特币私钥，共计0.00818975 BTC和30.40 XRP，这些资金仍保留在原始帐户中。

对于椭圆曲线离散对数问题，我们使用的攻击方法明显比天真的暴力攻击或最先进的算法快得多。可以使用像Pollard rho [28]这样的平方根时间算法，这样我们就可以找到我们找到的少量64位或128位nonce目标;比特币区块链中大约2 ^。攻击30个签名将需要比我们获得的更多的计算资源。相比之下，对于所有区块链，我们的计算总共耗费了40年的CPU时间（注意：CPU时间是CPU全速运行时完成整个过程所需的时间），这些计算都是用Python完成的。

nonce漏洞分为几个类，本研究表明我们已经发现了几个独立的实现漏洞。当使用的随机数比我们预期的短时，我们首先使用隐藏数问题算法来找到长期ECDSA签名密钥，并找到长度为64位，110位，128位和160位的随机数的密钥。

道德规范：除非实际计算易受攻击地址的实际私钥，否则我们无法验证这些漏洞的存在。对于加密货币，这些密钥允许我们或任何其他攻击者从相关帐户中窃取资金。对于ssh或https，这些密钥将使我们或任何其他攻击者能够模拟终端主机。我们没有这样做。在我们的研究中，我们没有转移任何加密货币或积极攻击自己。我们的研究完全是被动的，只需要观察交易或一般网络测量。但是，鉴于我们已经发现一些证据表明其他攻击者已通过已知漏洞清空相关的受损加密货币用户帐户，包括重复的nonce和在线发布私钥。我们预计，一旦这个缺陷被恶意攻击者利用，相关用户就会受到影响。

我们尝试向少数我们可以识别的团队披露这些缺陷，但在大多数情况下，我们无法向特定供应商，维护人员或用户披露这些漏洞。

对策。我们在本文中讨论的所有攻击都可以通过使用确定性ECDSA随机数生成工具来防止，该工具已经在默认的比特币和以太坊库中实现。

二，相关工作
 
隐藏号码问题和ECDSA。隐藏数字问题和我们用来解决它的基于格的算法是由Boneh和Venkatesan提出的，他用它来证明计算Diffie-Hellman最重要部分的难度。

Howgrave Graham，Smart [19]，Nguyen和Shparlinski [26]应用隐藏数字问题来证明如果攻击者可以学习一些最重要的签名nonce位，DSA和ECDSA签名方案就不安全。从那时起，这种技术已经在实践中应用于侧信道攻击。

重复的DSA/ECDSA签名。由于nonce的重复签名，许多研究工作已经检查了DSA和ECDSA中的漏洞。 Heninger，Durumeric，Wustrow和Halderman通过从SSH握手中搜索重复的DSA签名，在2012年公开了1％的SSH主机密钥。他们将问题追溯到在低资源设备上实现随机数生成。

Bos，Halderman，Heninger，Moore，Naehrig和Wustrow [7]在2013年比特币区块链中记录了经常性的随机数，作为椭圆曲线密码学更广泛研究的一部分。 Valsorda在2014年研究了重复的比特币nonce.Courtois，Emirdag和Valsorda在2014年研究了重复的比特币nonce，并指出它很可能对密钥造成威胁。 2016年，Castellucci和Valsorda研究了重复的nonce和弱密钥变体，以及比特币密钥中存在的重复nonce。 Brengel和Rosow在2018年从相同的密钥签名中研究了重复的nonce，并将比特币区块链中不同密钥签名之间泄露的nonce联系起来。

密码货币的密钥生成问题。 2013年，Android SecureRandom的一个主要漏洞被指控导致许多比特币Android Wallet用户被盗，这是由错误的随机数生成器生成重复的ECDSA签名随机数引起的。 2015年，Blockchain.info的Android应用程序被发现生成了重复的私钥，因为应用程序的种子是从random.org导出的，该网站有403个问题，并在几个月前重定向到它们。 Https网址。

密码货币的密码分析。大比特币对撞机是对比特币私钥的猛烈搜索，它使用相当线性的强力搜索算法，最多可搜索54个密钥。对于泄露的公钥，使用平方根离散对数算法[28,34]是一种更有效的方法来恢复这种短私钥，但目前我们还没有看到有人试图这样做。

三，椭圆曲线数字签名算法（ECDSA）
 
椭圆曲线数字签名的公共域参数包括有限域上的椭圆曲线E和E上第n阶的基点G.私有签名密钥是整数d模n，公共签名验证密钥是点Q=dG。椭圆曲线公钥可以通过提供公共点Q的x和y坐标来表示未压缩形式，或者可以通过仅提供x坐标和y值的单个奇偶校验位来表示为压缩形式。

为了对消息散列h进行签名，签名者选择每个消息的随机整数k模n来计算

3.1密码币中的ECDSA

比特币，以太坊和纹波都用在椭圆曲线secp256k1中。
通过使用sha-256和RIPEMD-160算法重复散列未压缩或压缩的ECDSA公钥来生成比特币地址。

以太坊地址是未压缩ECDSA公钥的Keccak-256哈希的最后20个字节，其中Keccak-256算法是SHA-3算法的早期版本。以太网公钥未明确提供签名。相反，签名包含一个额外的字节v，允许从签名派生公钥。

通过SHA-256和RIPEMD-160算法反复散列公钥并连接散列的各个部分来获得Ripple地址。

出于纸质分析的目的，在上述加密货币中，只有在为交易签名地址之后才会显示ECDSA公钥。

通过签名，比特币和Ripple将以未压缩或压缩格式显式显示ECDSA公钥;在以太坊中，客户端必须使用密钥恢复从签名本身派生公钥。

ECDSA签名用于验证交易的发件人。地址可以是单个签名，其对应于单个公钥，或多签名地址，其需要n个公钥集中的至少k个的有效签名来完成交易。通常，用户应该为每个事务使用新地址。

签名规范化。 ECDSA签名具有将使用相同公钥验证的签名（r，s）和（r，-s）的属性。 2015年10月，比特币通过在签名中使用较小的s和-s mod n值来引入签名过程中的更改，以使签名唯一。以太坊和瑞博也进行了这种类型的签名规范化，这将影响我们的攻击。

3.3对ECDSA的基本攻击

如果攻击者知道用于生成ECDSA签名的每条消息（每条消息）的随机数k，则长期密钥d很容易计算，因为

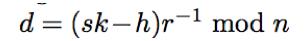
众所周知，如果使用相同的随机数k来使用相同的密钥对两个不同的消息h1和h2进行签名，则将显示该密钥。令（r1，s1）是在消息散列h1上生成的签名，并且（r2，s2）是消息散列h2上的签名。我们立即得到r1=r2，因为r1=r2=x（kG）。然后我们可以如上所述计算和恢复密钥。

四，对ECDSA的格攻击
 
在随机模n上，签名随机数k也必须完全相同。否则，可以使用解决隐藏数问题的技术来解决密钥d。

有关具体的攻击说明，请参阅原始论文。

后记：对于加密货币持有者来说，最重要的是掌握保管的安全方式和生成私钥的方式。选择一个好钱包非常重要。虽然官方钱包“笨重”，但相对更安全。